A Blog Post about Query Execution Engines

Posted: September 4, 2016 | Author: | Filed under: Research | Tags: , , , , | Leave a comment

Recently, I joined a team blog for sharing knowledge and experiences with nice guys. In the blog, I wrote a blog post about query execution engines at
A Survey of Query Execution Engines (from Volcano to Vectorized Processing). Enjoy!

데이터베이스 시스템의 주제별 기초 논문들

Posted: May 25, 2015 | Author: | Filed under: Research | Tags: , | Leave a comment

데이터베이스 시스템 이라는 큰 주제 아래 각 세부 주제에 대한 기초 논문 목록 들이다. 한참 학교에서 공부하던 시절에 정리하고 틈틈히 업데이트 했던 것 같다. 추후에 data processing이나 column store에 대한 논문들도 공유하도록 하겠다.

데이터베이스 분야는 일반적으로 순수한 알고리즘이나 자료구조 부터 다양한 응용 문제나 이론까지 아주 광범히 하다. 말 자체는 ‘데이터베이스’라서 약간은 고리타분해 보이기도 하지만 데이터에 대해 일반화 가능한 모든 연구라고 봐도 무방할 만큼 해당 학계에서 다양한 연구를 다룬다. 최근 큰 인기를 얻고 있는 하둡이나 분산 데이터처리 역시 데이터베이스 분야에서 활발히 다루어지고 있다. 마이닝의 많은 연구들 또한 이 분야에서 다루어진다. 제목에서 언급한 ‘데이터베이스 시스템’이라고 하면 일반적으로 시스템 구현기술과 이론에 해당되는 내용을 말한다.

개인적으로 해당 분야나 문제를 접할 때 그 문제에 대한 가장 초기 논문들은 꼭 읽어보려고 노력한다. 그 이유는 그 논문들이 그 문제에 대해 가장 깊은 통찰력과 고민들을 많이 담고 있기 때문이며 후대의 논문들 일수록 초기 논문들이 한 고민이나 통찰은 기본적인 전제로 사용되고 문제 풀이 아이디어 위주로 기술되기 때문이다. 그래서 아래 리스트는 각 분야의 초기 논문들 및 전체를 정리하는 논문들 위주로 리스팅이 되어 있다.

주제별로 중요한 논문을 다 담긴 것은 아니다. 주로 내가 관심 있었던 것들 위주이다. 또한 See Also에는 대학들의 좋은 커리큘럼이나 읽어볼만한 주제별 논문에 대해 정리한 리스트의 링크를 담고 있다. 그리고 그 동안은 개인적인 위키에 업데이트를 했었는데 앞으로는 이곳에서 업데이트를 하도록 하겠다.

History

  • M. Stonebraker and J. M. Hellerstein, “What Goes Around, Comes Around,” in Readings in Database Systems, 2005, pp. 2-41.
  • J. M. Hellerstein and M. Stonebraker, “Anatomy of a Database System,” in Readings in Database Systems, 2005, pp. 42-95.
  • Thomas Haigh, Fifty Years of Databases, ACM SIGMOD Blog, 2012.

Architecture

  • M. M. ASTRAHAN et al., System R: relational approach to database management, ACM TODS, 1976.
  • Donald D. Chamberlin et al., A History and Evaluation of System R, Communications of the ACM, 1981.
  • Michael Stonebraker et al., The Design and Implementation of Ingres, ACM TODS, 1976.
  • Joseph M. Hellerstein, Michael Stonebraker, and James Hamilton, Architecture of a Database System, Foundations and Trends in Databases, 2007.

Query Processing

Access Method

  • P. Griffiths Selinger et al., Access Path Selection in a Relational Database Management System, ACM SIGMOD, 1979.
  • Jim Gray et al., The Five-Minute Rule Ten Years Later, and Other Computer Storage Rules of Thumb, ACM SIGMOD Record, 1997.

Transaction Management

Logging

  • C. Mohan et al., ARIES: A Transaction Recovery Method Supporting Fine-Granularity Locking and Partial Rollbacks Using Write-ahead Logging, ACM TODS, 1987.
  • C. Mohan, Repeating History Beyond ARIES, VLDB Conf, 1999.
  • Russel Sears et al,, Segment-Based Recovery: Write-ahead logging revisited, PVLDB, 2009.
  • Philip L. Lehman et al., Efficient Locking for Concurrent Operations on B-Trees, ACM TODS, 1981.

Concurrency Control

  • Jim Gray et al., Granularity of Locks and Degrees of Consistency in a Shared Data Base, Readings in database systems, 1976.
  • Concurrency Control in Database Systems, ACM Computing Survey, 1981.
  • H. T. Kung, On optimistic methods for concurrency control, ACM TODS, 1981.
  • Rakesh Agrawal et al., Concurrency Control Performance Modeling: Alternatives and Implications, ACM TODS, 1987.
  • C. Mohan et al., Transaction Management in the R* Distributed Database Management System, ACM TODS, 1986.
    • Two Phase Commit

Data Warehouse

  • Surajit Chaudhuri and Umeshwar Dayal., An Overview of Data Warehousing and OLAP Technology, ACM SIGMOD Record, 1997.
  • Patrick O’Neil and Dallan Quass, Improved Query Performance with Variant Indexes, ACM SIGMOD, 1997.
  • Jim Gray et al., Data Cube: A Relational Aggregation Operator Generalizing Group-by, Cross-Tab, and Sub Totals, Data Mining and Knowledge Discovery, 1997.
  • Yihong Zhao et al., An Array-Based Algorithm for Simultaneous Multidimensional Aggregates, ACM SIGMOD, 1997.
  • C. Mohan and Inderpal Narang, Algorithms for creating indexes for very large tables without quiescing updates, ACM SIGMOD, 1992.

See Also

A Brief Introduction to Skyline Problem (Pareto-optimal Tuples) (1)

Posted: September 6, 2009 | Author: | Filed under: Research | Tags: , , , , | 1 Comment

The skyline problem is to compute the best tuples from a set of ordered d-tuples. The name is originated from what the solution represented on 2d plane resembles the scene that urban buildings comprise. Skyline is one of the recommendation queries, and it is considering multi criteria. It is very interesting problem as well as very useful query. This problem has been being intensively studied for recent years. Today, I’m going to present the problem definition of skyline. Next time, I’ll describe several algorithms for the skyline problem.

Singapore Skyline (#12) First of all, let us know the input data. The input data D^{d} of skyline is a set of n ordered d-tuples, each of which consists of ordered d scalar values. They are shown in below formulas:

D^{d} = {tp_{1},tp_{2},...tp_{n}}

tp_{i} = (v_{1},v_{2},...,v_{d})

tp_{i} denotes a d-tuple. And, we need to understand the definition of the dominance relation. In addition, because the skyline problem is to find the better tuples, we need an assumption about ‘better’. In most literature, it is assumed that the less value is better, so we follow this assumption.

Definition 1 (Dominance). Let tp and tp’ be tuples in D^{d} where v_{i} is an element of tp and u_{i} is an element of tp’ for 1 < i leq d. Then, tp dominates tp’ if and only if  forall{i}, v_{i} leq u_{i} land exists{j}, v_{j} < u_{j}.

In other words, it is said that one tuple tp dominates another tuple tp' if tp is not worse (not greater) than tp' in all dimensions and tp is better (less) than tp' in at least one dimension.

Definition 2 (Skyline) Given a data set D^{d}, a skyline contains tuples that is not dominated any other tuples in D^{d}.

As I described above definition, a skyline is a set of tuples and the tuples are not dominated by any other tuples in D^{d}. In literature, a d-dimensional data set and above two definitions are usually represented for comprehensive description to d-points on d-axies.

Without loss of generality, we assume that D^{d} is a 2d data set (i.e., d=2). A data set is given as follows:

  • a = (3,2)
  • b = (8,1)
  • c = (1,10)
  • d = (4,3)
  • e = (8,6)

Each element of a tuple in D^{d} can be represented to one axis. In other words, the first element and the second element of tuples are represented to X and Y axies respectively. Then, tuples of above list are represented to 2d points as shown in Fig. 1.

Fig. 1. An example of a skyline

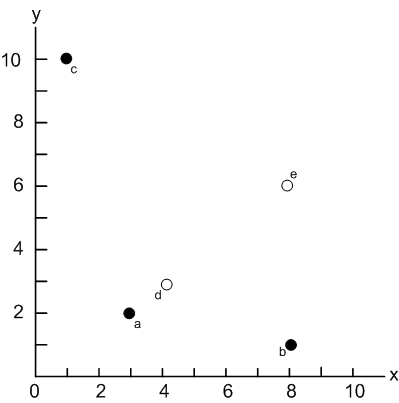
Fig. 1. An example of a skyline

In Fig. 1, let us look into a dominance relation. The point a dominates the points {d,e} since elements of the point a less than those of {d,e} in X and Y. The point b dominates only e since X values of {b,e} are same (i.e., X=8) but Y of b (i.e., 1) is less than that (i.e., 6) of e. The points {d,e} cannot belong to the skyline because they are dominated by other tuples. Consequently, the points a,b, and c belong to the skyline since they are not dominated by any other tuples.

Initially, the skyline problem was known as the maxima vector problem (H. T. Kung et. al 1975) for traditional processing system. However, this problem was revisited by the Skyline Operator (Stephan Börzsönyi et. al 2001). Since then, this problem has been intensively studied in database area.

Next time, I’ll describe several algorithms including above algorithms in detail.

← Older Entries