A Brief Introduction to Skyline Problem (Pareto-optimal Tuples) (1)
Posted: September 6, 2009 Filed under: Research | Tags: database, decision making, pareto tuples, query, skyline 1 CommentThe skyline problem is to compute the best tuples from a set of ordered d-tuples. The name is originated from what the solution represented on 2d plane resembles the scene that urban buildings comprise. Skyline is one of the recommendation queries, and it is considering multi criteria. It is very interesting problem as well as very useful query. This problem has been being intensively studied for recent years. Today, I’m going to present the problem definition of skyline. Next time, I’ll describe several algorithms for the skyline problem.
 First of all, let us know the input data. The input data
First of all, let us know the input data. The input data of skyline is a set of n ordered d-tuples, each of which consists of ordered d scalar values. They are shown in below formulas:
Definition 1 (Dominance). Let tp and tp’ be tuples in
where
is an element of tp and
is an element of tp’ for
. Then, tp dominates tp’ if and only if
.
In other words, it is said that one tuple dominates another tuple
if
is not worse (not greater) than
in all dimensions and
is better (less) than
in at least one dimension.
Definition 2 (Skyline) Given a data set
, a skyline contains tuples that is not dominated any other tuples in
.
As I described above definition, a skyline is a set of tuples and the tuples are not dominated by any other tuples in . In literature, a d-dimensional data set and above two definitions are usually represented for comprehensive description to d-points on d-axies.
Without loss of generality, we assume that is a 2d data set (i.e., d=2). A data set is given as follows:
- a = (3,2)
- b = (8,1)
- c = (1,10)
- d = (4,3)
- e = (8,6)
Each element of a tuple in can be represented to one axis. In other words, the first element and the second element of tuples are represented to X and Y axies respectively. Then, tuples of above list are represented to 2d points as shown in Fig. 1.
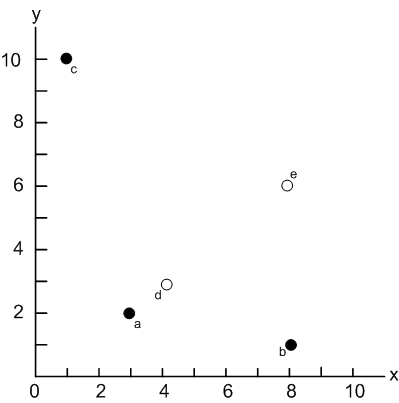
Fig. 1. An example of a skyline
In Fig. 1, let us look into a dominance relation. The point a dominates the points {d,e} since elements of the point a less than those of {d,e} in X and Y. The point b dominates only e since X values of {b,e} are same (i.e., X=8) but Y of b (i.e., 1) is less than that (i.e., 6) of e. The points {d,e} cannot belong to the skyline because they are dominated by other tuples. Consequently, the points a,b, and c belong to the skyline since they are not dominated by any other tuples.
Initially, the skyline problem was known as the maxima vector problem (H. T. Kung et. al 1975) for traditional processing system. However, this problem was revisited by the Skyline Operator (Stephan Börzsönyi et. al 2001). Since then, this problem has been intensively studied in database area.
Next time, I’ll describe several algorithms including above algorithms in detail.